

The higher ones of these rates really are astoundingly fast.
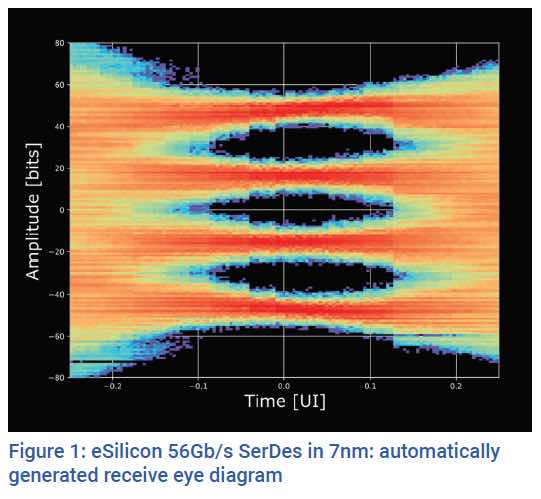
The optical internet forum (OIF) had defined some standard datarates for use with fiber, and everyone pretty much adopted the standard rates: 3.125G, 6G, 10G, 28G, 56G, and 112G (where G is actually gigabits per second).
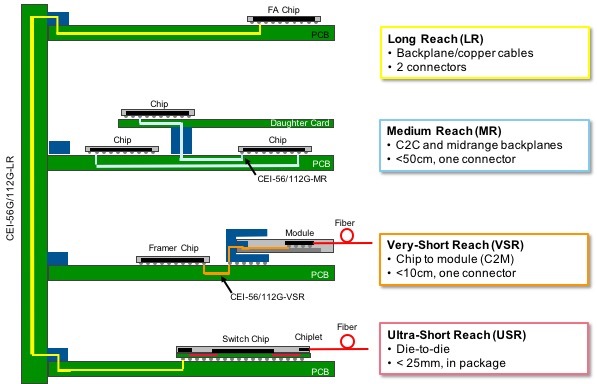
So the next development was to go to serial interfaces, and make up for the fact that you only had one or two pins by running them very fast.

I remember coding a device driver for a synchronous IBM box which ran over a twisted pair across to the Edinburgh University Computing Center. For example, the first Ethernet ran serially over coaxial cable. Of course, long-distance networks had always just had a single signal (well, usually two since you need a return path). Instead of using 64 pins to transfer a value, they could be transferred on a single pin at a much higher datarate. The final piece of the puzzle was to abandon trying to have clocked parallel interfaces, and switch to serial interfaces. One minor development was the approach taken with DDR memories where data was transferred on both edges of the clock (DDR stands for double data rate). It became more and more impossible to find enough pins to have clocked parallel interfaces where data was transferred only on clock edges. With 64 bits of address and 64 bits of data, that's already 128 pins even before worrying about anything else. That meant we could get a lot more pins onto a plastic package of the same size than putting all the pins around the edge.Īs address spaces went from 16 bits, to 32 bits, to 64 bits, the demand for pins was insatiable. This was done by Motorola in about 1990 (under the name overmoulded plastic carrier or OMPC). So the next advance was to invent the BGA. The first trick was to multiplex pins, essentially using the same pin for two different functions. I think the largest quad-flat-packs (QFP) had 256 pins. Until the invention of the ball-grid-array (BGA) we didn't have a huge number of pins to play with, so this was a problem. This is now known as Rent's Rule. We can combine Rent's Rule with Moore's Law, that the number of gates G doubled every two years, and so every two years the number of pins P grew by 1.4 ( √2). So the number of pins grows more slowly than the number of gates, but it grows inexorably. If R is 0.5 then the number of pins is proportional to √G, which is what I remember from my VLSI design classes. It usually has a value between 0.5 and 0.8. Actually, traditionally a Greek rho is used instead of R. It was a power law, where the number of pins was cG R where c and R are constants. Rent, who was working at IBM at the time, noticed a connection between the number of pins P on integrated circuits being use and the number of gates G on the integrated circuits.


 0 kommentar(er)
0 kommentar(er)
